3. Trigonometry
d. Trig Identities
7. Summary of Trig Identities
Here is a summary of the identities which are most useful throughout calculus. * = more important ** = most important
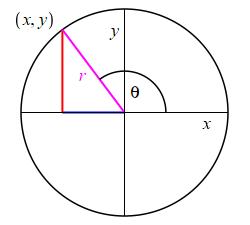
Circle Definitions
\[\begin{aligned} &\sin\theta=\dfrac{y}{r}\quad &&\cos\theta=\dfrac{x}{r} \qquad \qquad (**) \\[8pt] &\tan\theta=\dfrac{y}{x}\quad &&\cot\theta=\dfrac{x}{y} \\[8pt] &\sec\theta=\dfrac{r}{x}\quad &&\csc\theta=\dfrac{r}{y} \end{aligned}\]
Quotient and Reciprocal Identities
\[\begin{aligned} &\tan\theta=\dfrac{\sin\theta}{\cos\theta}\quad &&\cot\theta=\dfrac{\cos\theta}{\sin\theta}=\dfrac{1}{\tan\theta} \\[8pt] &\sec\theta=\dfrac{1}{\cos\theta}\quad &&\csc\theta=\dfrac{1}{\sin\theta} \end{aligned}\]Pythagorean Identities
\[\begin{aligned} &\sin^2\theta+\cos^2\theta=1 \qquad \qquad (**) \\ &\tan^2\theta+1=\sec^2\theta \\ &1+\cot^2\theta=\csc^2\theta \end{aligned}\]Parity Identities
\[\begin{aligned} \sin(-\theta)=-\sin(\theta) \qquad \cos(-\theta)=\cos(\theta) \qquad \qquad \quad (*) \end{aligned}\]Complementarity Identities
\[\begin{aligned} \sin\left(\dfrac{\pi}{2}-\theta\right)=\cos(\theta) \qquad \cos\left(\dfrac{\pi}{2}-\theta\right)=\sin(\theta) \qquad \quad (*) \end{aligned}\]Supplementarity Identities
\[\begin{aligned} \sin(\pi-\theta)=\sin(\theta) \qquad \cos(\pi-\theta)=-\cos(\theta) \end{aligned}\]Sum Identities
\[\begin{aligned} \sin(A+B)&=\sin(A)\cos(B)+\cos(A)\sin(B) \qquad \qquad (**) \\ \cos(A+B)&=\cos(A)\cos(B)-\sin(A)\sin(B) \qquad \qquad (**) \end{aligned}\]Difference Identities
\[\begin{aligned} \sin(A-B)&=\sin(A)\cos(B)-\cos(A)\sin(B) \\ \cos(A-B)&=\cos(A)\cos(B)+\sin(A)\sin(B) \end{aligned}\]Double Angle Identities
\[\begin{aligned} \sin(2A)&=2\sin(A)\cos(A) \qquad \qquad \quad \ (*) \\ \cos(2A)&=\cos^2(A)-\sin^2(A) \qquad \qquad (*) \\ &=2\cos^2(A)-1 \\ &=1-2\sin^2(A) \end{aligned}\]Square Identities
\[\begin{aligned} \sin^2(A)&=\dfrac{1-\cos(2A)}{2} \qquad \qquad (**) \\ \cos^2(A)&=\dfrac{1+\cos(2A)}{2} \qquad \qquad (**) \end{aligned}\]Law of Sines
Given a triangle with angles \(A\), \(B\) and \(C\) and opposite sides with lengths \(a\), \(b\) and \(c\): \[\begin{aligned} \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \end{aligned}\]
Law of Cosines
Given a triangle with angles \(A\), \(B\) and \(C\) and opposite sides with lengths \(a\), \(b\) and \(c\): \[\begin{aligned} c^2=a^2+b^2-2ab\cos C \qquad \qquad (**) \end{aligned}\]
The Triangle Inequality
Given a triangle with side lengths \(a\), \(b\) and \(c\): \[\begin{aligned} |a-b| \le c \le a+b \end{aligned}\]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum